Math Kids: Why do I have to learn this stuff? When will I ever use it? Read below to learn how mathematics can enter into nearly every corner of your life.

1. Spreading rumors
2. Risk: is it worth it?
3. Are you sure about that doc?
4. Art: packing three dimensions into two
5. Prime numbers and the National Security Agency
6. Make your parents promise to buy you a motorcycle
7. The story of 9 (learn how to multiply by nine using your fingers)
8. The story of 7 and 10 (learn how to multiply using your fingers)

SPREADING RUMORS

1. Problem. Your best friend tells you a secret and makes you promise not to tell anyone. Although you are just dying to tell someone, you don't really want your friend's secret to be widely known. Is there much harm in telling just two people?
   
   
2. Intuition. When spreading rumors, our sense is that there is little harm in telling just one or two people. We make them promise not to tell anyone else (in the same way that we promised), and figure it will stop there. Or, if they do tell someone, then the rumor won't spread very far. As we will see below, this is an example of where our intuition is quite poor: rumors spread very fast.
   
   
3. Math. You tell your best friend's secret to two people. Now, 4 people know the secret: you, your best friend, and the two people you just told. Let's assume that the two people to whom you told the secret each tell two people, for a total of four new people. Now, 8 people know the secret. If each of the last four people to receive the secret tell two people, eight new people know the secret. After four passes of the secret, a total of 16 people know the secret.
   
   
   
   
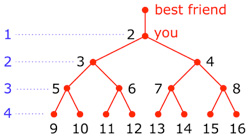
   This process continues: the group of people who just learned the secret, each tell two more people. After just ten passes, 1,024 people will know the secret, and after 20 passes, 1,048,576 people will know the secret. After 28 passes, 268,425,456 people know, which is roughly the population of the United States. And after 33 passes, more than 8.5 billion people will know, which is more than the population of the entire planet.
   
   The number of people who know a secret doubles after each pass (2, 4, 8, 16, 32, ...). That is, after N passes, 2N people know the secret. This is known as exponential growth.
   
   If we assume that each person will act in a similar manner to yourself, we see that the rumor will spread to a large number of people very quickly.
   
   
4. Summary. When holding a secret we believe that little harm is done by telling just a few people, since the number of people that know the secret has only increased by a small number. The problem, of course, is that everyone thinks like this, and everyone tells a few people. The number of people who learn of the secret, therefore, grows very quickly, at a exponential rate. Here are a few more surprising examples of the impact of exponential growth.
   
   
   1. Take a simple piece of notebook paper. Fold it in half. Fold it in half again, and again. How thick will the paper be after a total of 50 folds? A single sheet of paper is 0.1 mm thick. Folded once, the paper is 0.2 mm thick; folded twice it is 0.4 mm thick; folded three times it is 0.8 mm thick. The thickness is doubling each time (exponential growth). After ten folds, the paper is 102.4 mm thick (10.24 cm = 4.03 in). After twenty folds, the paper is 104,857.6 mm thick (approximately 105 m or 344 ft -- approximately the height of a 30-story building!). After 50 folds, the paper is 112,589,990,684,262.4 mm thick (approximately 112 billion km or 70 billion miles, almost the distance to the sun.
   2. Once upon a time there was a king who loved to play chess. One day the king proposed that if anyone in his kingdom could beat him at chess, the king would grant them any reasonable wish. A poor farmer stepped forward to meet the king's challenge. Much to the king's surprise, the farmer beat the king quickly and with seeming ease. True to his word, the king agreed to grant the farmer's wish. Wanting to wish for something that seemed reasonable, the farmer suggested the following: "I propose that you place on the first square of the chess board one penny, and on the second square, two pennies, on the third, four pennies, and so forth, until the last square is reached." After a moments thought, the king granted the request, as it seemed that the farmer had, in fact, asked for very little money. As the king began to place the money on the chess board, however, he soon realized his terrible mistake. Let's see why.
      
      The chess board consists of 8 x 8 = 64 squares. On the first row of the board, the king placed:
      
      0.01, 0.02, 0.04, 0.08, 0.16, 0.32, 0.64, 1.28
      
      for a total of $2.55. Notice that the amount of money is doubling between squares (exponential growth). On the second row, the king placed:
      
      2.56, 5.12, 10.24, 20.48, 40.96, 81.92, 163.85, 327.68
      
      Combined with the first row, there was a total of $655.35 on the board. On the third row, the king placed:
      
      655, 1310, 2621, 5242, 10485, 20971, 41943, 83886
      
      Combined with the first two rows, there was a total of $167,772.16 – and there were still five rows to complete! Continuing along like this, the completed board would have contained $368,934,881,474,191,032.32. The king, of course, ran out of money well before this and was unable to keep his promise.

RISK: IS IT WORTH IT?

1. Problem. You are thinking of cheating on your math test. If you cheat, and don't get caught, you will get a better grade. If you cheat, and get caught, you will fail the exam and get in trouble. Putting aside the moral and ethical issues, how do you decide if you should cheat or not?
   
   
2. Intuition. Your decision is based on what you expect to gain by cheating balanced against the chance of getting caught and the penalty for getting caught. Let's say that if you don't cheat, you expect to score 60/100 on your exam. If you do cheat you expect to score 100/100. We need to factor in one more thing. If you cheat and get caught, you will score 0/100 (let's ignore, for now, the other penalties associated with getting caught cheating). Naturally, you will decide to cheat if doing so will increase your exam score. But since you don't know beforehand if you will get caught or not, you don't know if cheating will yield a score of 100 or 0.
   
   
   
   
   
3. Math. Let's say that the chance of getting caught is 50%. This means that the probability of getting caught is 50/100 or 1/2. The way to think about probabilities is to imagine taking, and cheating on, a large number of exams. After taking all of these exams, you can expect to get caught 1/2 of the time. On half of the exams you will score 100 and on the other half you will score 0. So your average score is 50 (100 x 1/2 + 0 x 1/2). This means that on any single exam, your expected score, if you cheat, is 50. This is the score that we compare against the score you receive for not cheating, 60. In this case, cheating won't pay off.
   
   
   
   
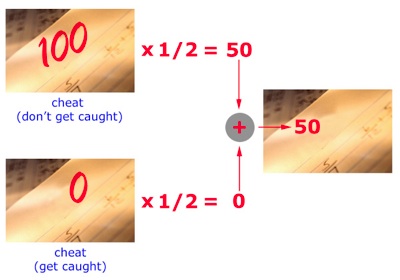
   Perhaps it seems strange to say that you expect to score 50 on the exam, since you will never actually receive a score of 50 (you will score 100 or 0). This expected score arises because of the uncertainty in getting caught - it allows us to combine the possible scores with their probabilities so that we have a single number upon which we can make a decision.
   
   Let's now say that the chance of getting caught goes down to 25%. In this case you will get caught 25/100 = 1/4 times, and not get caught 75% = 75/100 = 3/4 times. Your expected score now is 75 (100 x 3/4 + 0 x 1/4). In this case, cheating does pay off -- you can expect to gain an extra 15 points over not cheating.
   
   Now, let's factor in the other penalties for cheating. You will get in trouble with your teacher, principal and your parents. You might get detention, suspended, lose TV/video game privileges, etc. These should be factored into your decision. Let's say that the punishment is the equivalent of 200 exam points. Now, the score you receive for cheating and getting caught is -200 (instead of just 0). Your expected score now becomes 25 (100 x 3/4 - 200 x 1/4). In this case, cheating does not pay off because it is less than the score of 60 that you would receive by not cheating.
   
   
4. Summary. When faced with a decision where the outcome of one or more of your choices is uncertain, you can make a mathematically sound decision by combining the cost and probability associated with each option. The expected cost of any option is simply the probability times the cost. This strategy applies to many real-world situations:
   
   
   1. You can buy your favorite candy bar (A) for $2, or two of a new candy bar (B) for $1 each. Which should you buy? Let's assign a score of 100 to the pleasure of eating candy bar A. You have never tried candy bar B before, so you don't know if it will bring you more pleasure or not. Let's say that the probability of you liking candy bar B as much as A is 25% = 25/100 = 1/4. Then, the expected pleasure of candy bar B is 25 (100 x 1/4), and the expected pleasure of both of them is 50 (100 x 1/4 + 100 x 1/4). In this case, you should buy candy bar A – quality wins over quantity. If however, the price of candy bar B was just $0.25, then you could buy eight of them for $2, and your expected pleasure would be 200 (8 x 100 x 1/4), and you should try the new candy bar – quantity wins over quality.
   2. A lottery ticket costs $1 and the jackpot is $1,000,000. Should you buy the ticket? We need to compare the cost of the ticket ($1) with the expected payoff of buying the ticket. Let's say that the chance of winning is 1/50,000,000 (this is roughly the chance of winning the New York State lottery). The expected payoff is 2 cents (1,000,000 x 1/50,000,000). In this case, you should not buy a ticket.
   3. Your football team just scored a touchdown. You can kick a field-goal to add 1 point to your score, or try for 2 more points by running/passing the ball into the end-zone. Which should you do? Let's say that the probability of making the field-goal is 90% = 90/100 = 9/10, and that the probability of making the 2-point conversion is 25% = 25/100 = 1/4. Then, the expected payoff of the field goal is 0.9 points (1 x 9/10) and the expected payoff of the 2-point conversion is 0.5 (2 x 1/4). In this case, you should kick the field-goal (assuming that you are not down by 2 points with 10 seconds left on the clock).

ARE YOU SURE ABOUT THAT DOC?

1. Problem. During a routine check-up, your doctor runs a test that reveals that you have chicken pox. You know that the test might be wrong, so how do you determine the chance that you are actually sick?
   
   
2. Intuition. The doctor tells you that the test will report that you have chicken pox when you do not, one out of every 1,000 times. In other words, the test is 99.9% accurate, suggesting that there is a very good chance that you have chicken pox.
   
   The accuracy of the test, however, is not the only thing that we need to consider. We also need to consider the chance that you would be sick, regardless of the test. For example, a young boy tests positive on a pregnancy test that is wrong 1 out of 1,000 times. Surely we wouldn't say that the chance that he is pregnant is 99.9%. We need to consider the fact that it is impossible for him to be pregnant (test or no test).
   
   
3. Math. The probability that you are sick given a positive test result is the probability that the test result is positive given that you are sick, times the probability that you are sick (this is known as Bayes' rule, after the mathematician Thomas Bayes, 1702-1761). We can express this more formally as:
   
   P(S|T) = P(T|S) P(S)
   
   where P() denotes the probability of an event, S=you are sick, T=positive test result and "|" should be read as "given" (e.g., P(S|T) is the probability that you are sick given a positive test result).
   
   For example, the probability that the chicken pox test is positive given that you have chicken pox is:
   
   P(T|S) = 0.999
   
   this is the known error of the test. If your younger brother came down with the chicken pox, and you have never before had chicken pox, then the chance that you have chicken pox is pretty high, let's say 90%:
   
   P(S) = 0.90
   
   The overall probability that you have chicken pox is then:
   
   0.999 x 0.90 = 0.8991
   
   or just under 90%. If, however, you had chicken pox two years ago, and you have not come into contact with anyone with chicken pox, then the probability that you have chicken pox is low, let's say 20%:
   
   P(S) = 0.20
   
   The overall probability that you have chicken pox is then:
   
   0.999 x 0.20 = 0.1998
   
   or just under 20%, much smaller than the 99.9% based only on the test.
   
   
4. Summary. When evaluating the results of a medical test, you should take into consideration your inherent risk of having contracted whatever it is that you may have tested positive for. A surprising number of doctors don't understand this. So the next time the doctor returns to you a test result, ask them if their diagnosis has taken into consideration the full Bayesian likelihood.

ART: PACKING THREE DIMENSIONS INTO TWO

1. Problem. We live in a three-dimensional spatial world. Three dimensions because you can move left-right, up-down, and forward-backward. An artist's canvas is two-dimensional: the paint brush cannot move in the forward-backward direction when confined to the canvas. How then does an artist create a sense of three-dimensional space on a two-dimensional canvas?
   
   
2. Intuition. We perceive the buildings and road in the painting shown below as receding away from us, even though they are all simply flat objects on our computer screen. Our intuition probably tells us that the reason for this three-dimensional perception is that the buildings on the right (further from us, in depth) are painted smaller than those on the left (closer to us, in depth). Similarly, the road narrows as it recedes away from us.
   
   
   
   
   In as early as the 1400s, artists were conveying a sense of three-dimensional structure on a flat two-dimensional canvas. As we will see below, the key insight that led to this was the understanding of some simple geometry.
   
   
3. Math. Shown below is a diagram of how an artist might map a three-dimensional shape onto a two-dimensional canvas. In the lower part of the diagram, the object (red rectangle) is closer to the artist. In this case, the "image" of the object on the canvas is larger than when the object is further. That is, in order to convey a sense of three-dimensional structure, nearby objects should be drawn larger than distant objects. The precise difference in size is determined by geometry.
   
   
   
   
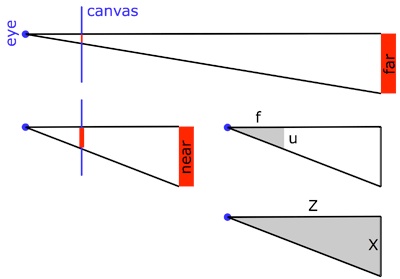
   Notice that in the above diagram we have a pair of similar triangles (gray). The ratio of the sides of similar triangles are equal, meaning that u/f = X/Z or u = fX/Z . That is, the size of the object on the canvas, u, is inversely proportional to its distance Z. This equation, known as perspective projection, specifies how large an object, that is a given distance from you, should be drawn.
   
   Shown below is an example of how to sketch a box under perspective projection to give the correct sense of three-dimensional structure.
   1. Draw a horizontal line (red). This is the horizon, and the ends of the line are the vanishing points. Draw a single vertical line (black). This is the front edge of the box. Connect the ends of this line to the vanishing points.
   2. Draw a vertical line (black) inside of the triangle formed by the lines extending from the left-most vanishing point. This is another edge of the box. Connect the ends of this vertical line to the right-most vanishing point (gray).
   3. Repeat the above step for the other side of the box. iv.Erase the horizon and guidelines, leaving behind a sketch of a three-dimensional box.
   
   
   
   
   
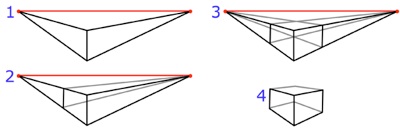
4. Summary. An artist's canvas is two-dimensional. And yet, artists are capable of giving us a sense of the three-dimensional space of the scene being painted. This is accomplished by painting nearby objects larger than more distant objects. The rules of geometry guide an artist in achieving the correct proportions in their paintings.
   
   

PRIME NUMBERS AND THE NATIONAL SECURITY AGENCY

1. Problem. The National Security Agency (NSA) wants to be able to send email in such a way that if somebody intercepts the message, they will not be able to read the message. And at the same time, the person for whom the message was intended should be able to read the message.
   
   
2. Intuition. In order to send a message that nobody but the intended party can read, the sender and receiver need to agree upon some kind of code so that a message can be scrambled and un-scrambled. The message "meet in prague on oct eleven at ten", for example, could be scrambled to read "teem ni eragup no tco nlevee ta net". Here, the first and last letters were switched. If this scrambled message were intercepted, its contents would not be immediately obvious. But, it probably wouldn't take long for somebody to break the code and decipher the message.
   
   The NSA, therefore, needs a code that makes it is easy for the sender to encode a message, and for the receiver to decode the message, but that is very difficult for anybody else to decode.
   
   
3. Math. A commonly used code for sending secure messages is known as RSA encryption. There are three basic steps:
   
   
   1. Generate "keys"
      • - select two large prime numbers, p and q
      • - compute the product of the two primes, n = pq
      • - compute the following product, m = (p-1)(q-1)
      • - choose a number e so that the greatest common divisor of e and m is 1
      • - compute d so that 1 < d < e and ed mod m = 1 (ed mod m is the remainder of dividing ed by m as many times as evenly possible)
   2. Scramble message (encryption)
      • - convert each letter of the alphabet to a number (a=1, b=2, c=3, ..., z=26, A=27, ..., Z=52)
      • - replace each letter of the message, x, with y = x^e mod n (^ means raise x to the power e)
      • - send the scrambled message, y
   3. Unscramble message (decryption)
      • - replace each letter of the received message, y with y^d mod n
      • - the result will be the original text message
   
   
4. Summary. Mathematicians and computer scientists have figured out a clever code for sending secrets that, for now at least, is very very difficult to break. The code relies on the simple numerical property that it takes computers a very very long time to factor large numbers into a product of prime numbers.
   
   The NSA (and others) is, by the way, trying to develop a special type of computer known as a quantum computer that, if it can be built, will be able to break this code.

MAKE YOUR PARENTS PROMISE TO BUY YOU A MOTORCYCLE

1. Problem. You want a motorcycle, but your parents won't let you buy one.
   
   
   
   
   
2. Intuition. Your parents are unlikely to simply agree to buy you a motorcycle. And it is unlikely that you can convince them to do so by cleaning your room, taking out the garbage, being nice to your little brother, etc. You need to get them to agree to buy you a motorcycle, without them knowing that they are doing so.
   
   
3. Math. If your parents are true to their word, all it will take for them to agree to buy you a motorcycle is to have the following conversation with them.
   
   you "Will you promise to hug me if I make a true statement and not hug me if I make a false statement?"
   parents "Uh, sure."
   you "You will neither give me a hug nor will you buy me a motorcycle."
   
   That's it. Now, explain to your parents their options:
   1. Your parents hug you, but they don't buy you a motorcycle. If your parents hug you, then your statement ("no hug, no motorcycle") will be false. But your parents agreed not to hug you if you made a false statement – so this option is no good.
   2. Your parents don't hug you, and they don't buy you a motorcycle. In this case, your statement ("no hug, no motorcycle") will be true. Your parents agreed to hug you if you made a true statement. But we just agreed above that they can't hug you – so this option is no good.
   3. Your parents hug you, and they buy you a motorcycle. In this case, your statement ("no hug, no motorcycle") is false. But your parents agreed not to hug you if you made a false statement – so this option is no good.
   4. And lastly, your parents don't hug you, but they buy you a motorcycle. In this case, your statement ("no hug, no motorcycle") is false. Since your parents agreed not to hug you if you made a false statement, there is no contradiction here.
   
   Option (4) is the only option that is consistent with your parent's promise, so they must buy you a motorcycle if they are to keep their promise to you.
   
   The above is an example of the application of a branch of mathematics known as logic. We can simplify the above statements with a few mathematical symbols:
   
   
   • H = your parents hug you
   • ~H = your parents don't hug you
   • M = your parents buy you a motorcycle
   • ~M = your parents don't buy you a motorcycle
   • S = (~H and ~M) – this is your statement
   • T = a true statement
   • F = a false statement
   
   Your parents promised that (if S=T then H) and (if S=F then ~H). We can now write the four options as follows (the symbols in red show the contradiction):
   
   
   • (H and ~M) implies S=F implies ~H
   • (~H and ~M) implies S=T implies H
   • (H and M) implies S=F implies ~H
   • (~H and M) implies S=F implies ~H
   
   Only the last option has no contradiction.
   
   
4. Summary. The above "trick" worked because we created a set of logical statements that led to contradictions in all but the desired conclusion. The logic of these statements is made particularly obvious when the statements are replaced with concise symbols.
   
   By the way, I doubt that this will actually convince your parents to buy you a motorcycle. But, maybe your parents will be sufficiently impressed with how clever you are, that you can convince them to buy you a video game as a consolation for them breaking their promise.